Visualizing Quadratic Form

quadratic form

• The quadratic form of M (M is symmetric) is $x^{T}Mx$

A symmetric matrix M

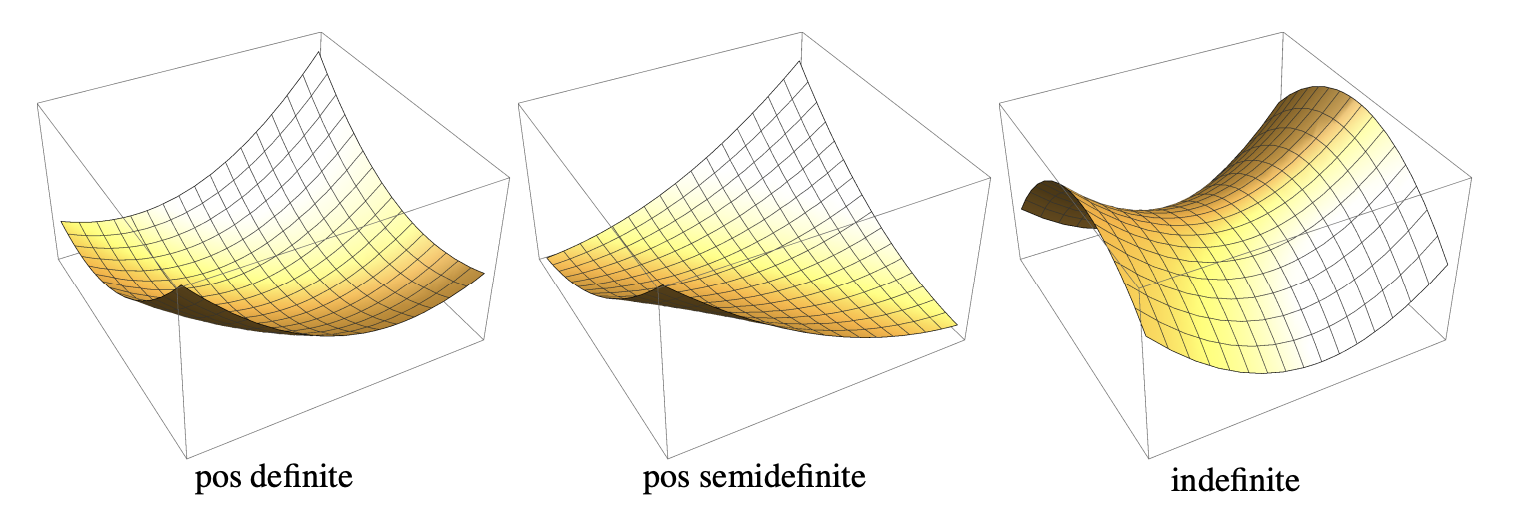
• is positive definite if $w^{T}Mw>0$ for all w $\ne$ 0 $⟺$ all eigenvalues are positive.
• A symmetric matrix M is positive semi-definite if $w^{T}Mw\ge 0$ for all w $\ne$ 0 $⟺$ all eigenvalues are non-negative. (Not invertible if eigenvalue 0)
• Indefinite: Saddle → if positive eigenvalues and negative eigenvalues.
• Invertible if there is no 0 eigenvalue.

---

Transformation by the matrix in quadratic form

Goal: Want the matrix such that it transforms the left graph to the right graph.

$$q_2(Az)=q_1(z)$$

Thus, $x=Az\text{and}z=A^{-1}x$

$q_2(x)=q_1(z)=q_1(A^{-1}x)=\Vert A^{-1}x{\Vert }^2=x^T{A}^{-1}{A}^{-1}x=x^T{A}^{-2}x$

Now that we have this equation, $q_2(x)=x^T{A}^{-2}x$, we can plot iso-contours of $q_2(x)$

Isocontours of a Quadratic Form

Given a symmetric PSD $\mathbf{M}$ and $q(x)=x^{T}Mx$, then the isocontours of $q(x)$ are

$$x^{T}Mx=c,\text{for}c\in R$$

• The axes of the ellipsoid are given by the eigenvectors of M
• The radii are determined by the square roots of the eigenvalues of $M^{-1/2}$. This is the same as radii = $\frac{1}{\sqrt{\lambda (M)}}$ because $\lambda (A^{-1/2})=\frac{1}{\sqrt{\lambda (A)}}$
• For Identity Matrix, isocontours are simply spheres.
• For Diagonal Matrix, isocontours are axis-aligned (same as coordinate axes).
• For General PSD, the isocontours are ellipses / ellipsoids.

In the case of $x^T{A}^{-2}x$, radii of ellipsoid = $\frac{1}{\sqrt{\lambda (A^{-2})}}=\lambda (A)$. The pattern here is therefore:

$M\to M^{-1/2}$ $M^{-2}\to M$

(multiply the exponent with $-\frac{1}{2}$) for eigenvalues (radii of ellipsoids)

---

{TODO: Discussion 5}

Recap on Symmetric Matrix and relate to the Quadratic form plot.

A symmetric matrix M

• positive definite \iff$$w^TMw > 0 for all $w\ne 0$ $⟺$ ${\lambda }^{\prime }s>0$.
• positive semi-definite $⟺$ $w^{T}Mw\ge 0$ for all $w⟺{\lambda }^{\prime }s\ge 0$ .
• indefinite $⟺$ have both +ve and -ve eigenvalues.
• invertible $⟺$ no 0 eigenvalue.

> [!cite] Shewchuk > > If M is only positive semidefinite, but not positive definite, the isosurfaces are cylinders instead of ellipsoids. These cylinders have ellipsoidal cross sections spanning the directions with nonzero eigenvalues, but they run in straight lines along the directions with zero eigenvalues.

---

{TODO: }

Every square matrix has to be Positive Semidefinite, including $A^{-2}$. If $A^{-2}$ exists, it is Positive Definite.

---

Isotropic = Variance is the same in all directions.

---