Ridge Regression (Tikhonov Regularization)

Optimization Problem

Find w that minimizes:

$$\Vert Xw-y{\Vert }^2+\lambda \Vert w^{\prime }{\Vert }^2=J(w)$$

where $w^{\prime }$ is the weight without the bias term or bias term 0.

• $l_2$ penalization promotes shrinkage of the weights. i.e. it will encourage our solutions to have smaller weights.
• Also makes the least squares problems to always have a unique minimum solution because of the $\lambda$ term — making the matrix to be Positive Definite instead of just Positive Semidefinite.

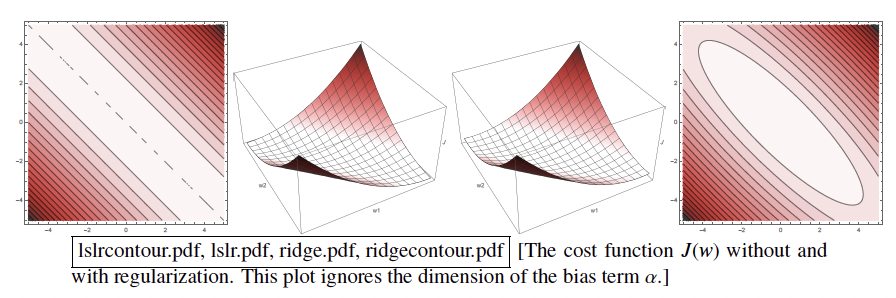
Left figure: ill-pose, many minima. Right figure: well-pose, one unique minima.

$l_2$ regularization reduces overfitting by reducing the variance while increasing the bias. In general, we don’t like big weights if the data and label are relatively smaller.

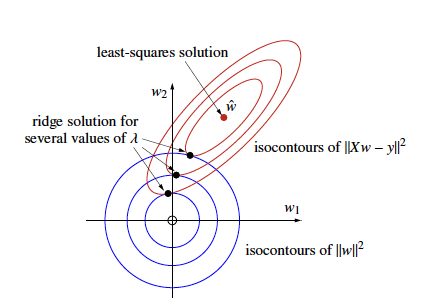
The Ridge Regression solutions lie at the tangent between the red isocontour and the blue isocontour. Notice how higher $\lambda$ would pull the solution towards the $\Vert w{\Vert }_2^2$ minimum.

---

If we were to solve the optimization problem:

$$argmi{n}_w\Vert Xw-y{\Vert }_2^2+\lambda \Vert w^{\prime }{\Vert }_2^2$$

The optimal solution would be:

$$(X^{T}X+\lambda I^{\prime })w^{\ast }=X^{T}y$$

Note that $X^{T}X+\lambda I^{\prime }$ is always Positive Definite and thus invertible - leading to a unique solution. $I^{\prime }$ is an identity matrix with the bottom right element being 0 (due to the fact that we don’t penalize the bias term).

---

Connection of Ridge Regression and Variance

Assume that the true data model is defined as $y=Xv+e$, where e is noise from a Normal Distribution. Then, the variance of the Ridge Regression at a test (arbitrary) point is:

$$Var(z^T(X^{T}X+\lambda I^{\prime }{)}^{-1}{X}^{T}e)$$

As $\lambda$ goes to $\infty$, variance approaches 0, but the bias increases. In practice, we need to tune the $\lambda$ by cross-validation.

Important Note: Features should be normalized so that the weights get penalized in the same amount, and the features will have same variance.

An Alternative way to achieve is this to use a different diagonal matrix instead of $\lambda I^{\prime }$, which will weight dissimilar amount to different features.

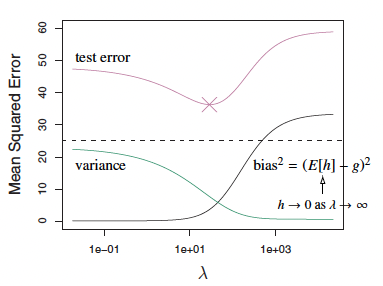
Bias Squared vs Variance as lambda increases.

Warning

$$\text{Variance}\propto \frac{1}{\text{\# of sample points}}\propto \frac{1}{\lambda }$$

---