Pseudoinverse of a Matrix

Tldr

• When a matrix is square and invertible, you know you can compute the inverse $A^{-1}$. But when the matrix is not square (e.g., tall or wide) or singular (non-invertible), you can’t compute a normal inverse.
• Instead, you can compute something called a pseudoinverse, denoted as $A^{†}$.

---

Moore-Penrose Conditions

1. $A{A}^{†}A=A^{†}$
2. $A^{†}A{A}^{†}=A$
3. $(A{A}^{†}{)}^T=A{A}^{†}$
4. $(A^{†}A{)}^T=A^{†}A$

---

• Pseudoinverse exists for any matrix, and acts like an inverse “as much as possible.”
• It helps solve the least square problem even when $A$ is not nice.
  • If $A$ is a $m\times n$ full column rank matrix and $m>n$, then $A^{†}$ gives the least-squares solution. | overdetermined system.
  • If $A$ is a $m\times n$ full row rank matrix and $n>m$, there are infinitely many solutions; but $A^{†}$ gives the minimum norm solution. | underdetermined system.
  • If A is a square matrix, $A^{†}=A^{-1}$.

---

Calculating the Pseudoinverse of a Matrix.

For a given $m\times n$ matrix $A$, the pseudo-inverse of it is defined as:

$$\begin{array}{rl}A& =U\Sigma V^T\\ A^{†}& =V{\Sigma }^{†}{U}^T\end{array}$$

${\Sigma }^{†}$ is obtained by taking the reciprocal of each non-zero singular value in $\Sigma$ and transpose it.

If ${\Sigma }^{m\times n}\to {{\Sigma }^{†}}^{n\times m}$

Warning

If we use compact SVD, then ${\Sigma }^{†}={\Sigma }^{-1}$.

---

I am a little bit lazy with typing this. But here is a good summary by ChatGPT regarding the connection between Pseudoinverse and four fundamental subspaces.

Important

If both $A$ and $A{A}^{†}$ project onto the column space of $A$, how are they different?

---

• Given a Compact SVD $X=U\Sigma V^T$,
• Null(X) = Null($V^T$) = Span($V_o$).
• Row(X) = Row($V^T$) = Span($V_r$).
• $X^{†}=V\Sigma U^T$
• Null($X^{†}$) = Null($U^T$) = Null($X^T$)
• Null($(X^{†}{)}^T$) = Null($V^T$) = Null($X$)
• Row($X^{†}$) = Col($X$)
• Col($X^{†}$) = Row($X$)
• $X,U,V,X^{†},X{X}^{†},X^{†}X$ all have the same rank r.

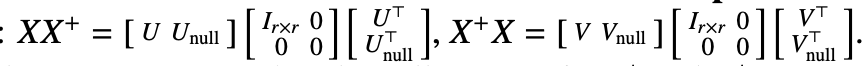
Notice that this expression is the same as eigenvalue decomposition form.

Therefore, we can say that the first r columns of $U$ are eigenvectors of $X{X}^{†}$ with eigenvalues 1, and the rest are eigenvectors with eigenvalue 0.

---