Principal Component Analysis

• Principal Component Analysis is an Unsupervised Learning i.e. we have sample points, but we don’t have labels.
• Therefore, no classes, no regressions, since there’s no y values. Nothing to predict.
• What we want to do is Discover some sort of underlying structure in the data.

---

Popular Techniques of unsupervised learning

1. Clustering: Partition data into groups of similar / nearby points.
2. Dimensionality reduction: Data often lies near a low dimensional subspace (or manifold) in feature space. Think about matrix low-rank approximation (SVD).
3. Density Estimation: Fit a continuous distribution to discrete data.

---

https://medium.com/@sebastiannorena/pca-principal-components-analysis-applied-to-images-of-faces-d2fc2c083371

Principal Component Analysis (PCA) Karl Pearson, 1901

Principal Component Analysis lies under Dimensionality Reduction.

Given sample points in ${\mathbb{R}}^d$, find k directions that capture most of the variation.

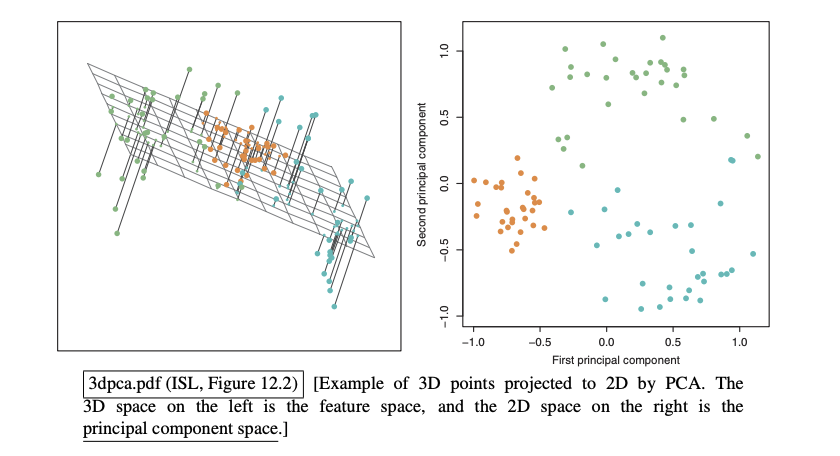
Left is the Feature Space and Right is the Principal Component Space

---

Example of PCA on hand-written digits (28 x 28) grayscale bitmaps.

One image = 784 dimensional vector → PCA → 2 dimensional vector

As we can see here, the two dimensions may not be enough to capture all the information | the two dimensions may not be enough to maximize the projected data point variance.

Why do we do PCA?

1. Reducing number of dimensions makes some computations cheaper. (e.g. regression).
2. Identify and remove irrelevant dimensions to reduce overfitting in learning algorithms. Subset selection; but the features are not axes-aligned. i.e. the new features are not the original features. PCA “combine” several input features into one or more orthogonal “new” features known as principal components.
3. Find a small basis for representing variations in complex things (faces, genes).

---

• Let Xbe n x d design matrix. No fictitious dimension.
• Center the X and also call it X. So, ${\sum }_{i=1}^n{x}_i=0$ Find the average across rows, which gives you the mean of each feature.
• Let w be a unit vector and $\tilde{x}$ be the projected data point. The Orthogonal projection of point x onto vector w is $\tilde{x}=(x\cdot w)w$
• If w is not unit vector, then $\tilde{x}=\left(\frac{x.w}{\Vert w{\Vert }^2}\right)w.$
• The idea is to pick the best w in the sense that w vector captures the original data the most.
• Given orthonormal directions $v_1,\dots ,v_k,\tilde{x}={\sum }_{i=1}^k(x\cdot v_i)v_i$. $\tilde{x}$ is the linear combinations of vectors $v^{\prime }s$.
• The $v^{\prime }s$ are not necessarily in the feature space since they’re principal components. Often we just want the k principal coordinates $x\cdot v_i$ in principal component space (just the coefficient; not the entire vector).
• We can compute these principal component directions from eigenvalues of $X^{T}X$ which are PSD $d\times d$ matrices.
• The eigenvalues of $X^{T}X$ are all $\ge$ 0. Sort them in the order of $0\le {\lambda }_1\le \cdots \le {\lambda }_d$.
• Let $v_1,\dots ,v_d$ be the corresponding orthogonal unit eigenvectors. These are the Principal components.

---

There are Three ways to derive PCA:

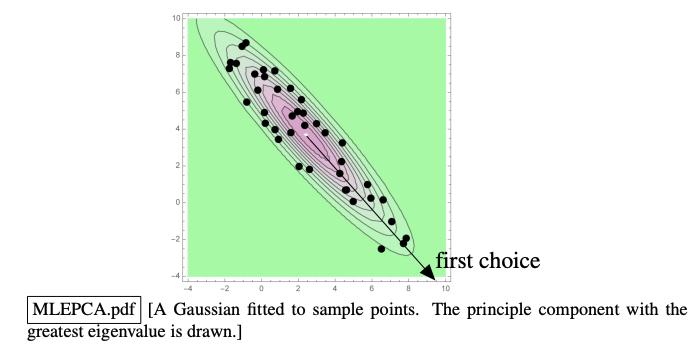
1. Fit a Gaussian to data with maximum likelihood estimation.

1. Choose k Gaussian axes of greatest variance.
2. Recall that MLE estimates a covariance matrix $\hat{\Sigma }=\frac{1}{n}{X}^{T}X$.

2. Find direction w that maximizes sample variance of the projected data.

1. Recall Rayleigh Quotient
2. The variance of the projected vectors is $\text{Variance}=\frac{1}{n}{\sum }_{i=1}^n(x_i^{T}w-\mu {)}^2$
3. Therefore, Variance is $\frac{1}{n}{\sum }_{i=1}^n{\left(x_i\cdot \frac{w}{\Vert w\Vert }\right)}^2$
4. $=\frac{1}{n}\frac{\Vert Xw{\Vert }^2}{\Vert w{\Vert }^2}=\frac{1}{n}\frac{w^T{X}^{T}Xw}{w^{T}w}$
5. $X^{T}X$ is a Positive Semidefinite matrix, and therefore, we can apply Rayleigh Quotient.
6. Thus, to maximize the Variance of the projected data points is the same as:
7. ${\text{maximize}}_w\frac{1}{n}\frac{w^T{X}^{T}Xw}{w^{T}w}$
8. From Rayleigh Quotient, the optimal solution for this optimization problem(maximize) is $p^{\ast }={\lambda }_{max}(X^{T}X)$
9. The optimal direction www is the eigenvector corresponding to the largest eigenvalue of $X^{T}X$.
10. If ${\lambda }_d$ is the largest eigenvalue of $X^{T}X$, then the maximum variance will be $\frac{{\lambda }_d}{n}$.
11. Therefore, eigenvector $v_d$ corresponding to the largest eigenvalue ${\lambda }_d$ is the first principal component.
12. If we constrain w to be orthogonal to $v_d$, we get the second principal component $v_{d-1}$.
13. Alternatively, using SVD, this corresponds to subtracting ${\sigma }_d{u}_d{v}_d^T$ (rank-1 approximation) from the original matrix $X$, and applying the same procedure on the residual matrix.

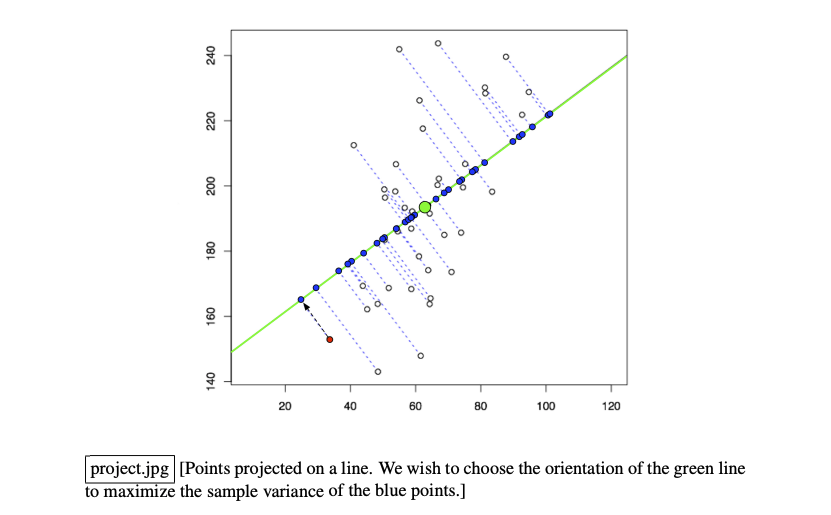
The blue dots are the projected points and we want to maximize the variance of them.

3. Find direction w that minimizes mean squared projection distance

• Similar to Least Square, they both minimize the mean squared distance.
• In Least Square, we measure the distance in y direction.
• In PCA, we measure the distance from training point to the subspace (hyperplane), perpendicular distance.
• Find w that minimizes ${\sum }_{i=1}^n\Vert x_i-{\tilde{x}}_i{\Vert }^2$
• $={\sum }_{i=1}^n{\Vert x_i-\frac{x_i\cdot w}{\Vert w{\Vert }^2}w\Vert }^2$
• $={\sum }_{i=1}^n\left(\Vert x_i{\Vert }^2-{\left(x_i\cdot \frac{w}{\Vert w\Vert }\right)}^2\right)$
• $=\text{constant}-{\sum }_{i=1}^n{\left(x_i\cdot \frac{w}{\Vert w\Vert }\right)}^2$
• This is the same as maximizing the latter term, which is the same as maximizing n x the variance of the project points (from part 2).
• Minimizing the mean squared projection distance = Maximizing the variance of the projected data points.

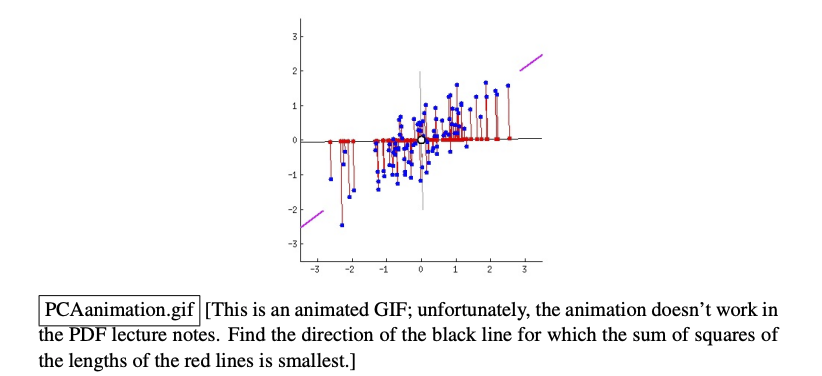
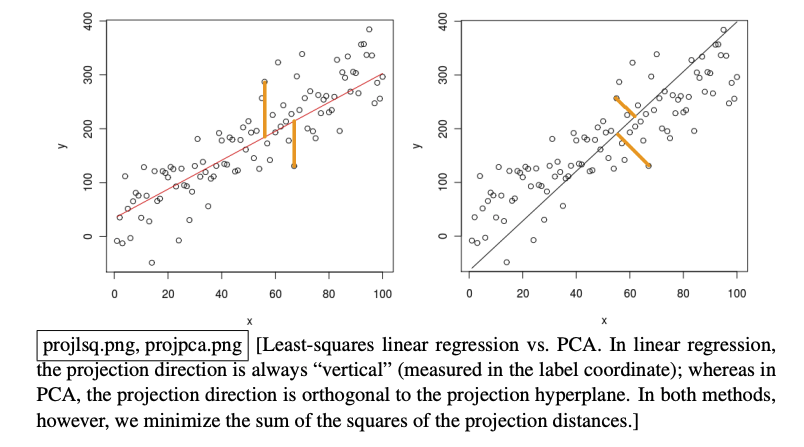
Least Squares Vs Principal Component Analysis Distances

---

PCA Algorithm:

# center matrix X
mean = np.mean(X, axis=0)
X_centered = X - mean
 
# normalize X (Optional: units of measurement different?)
	# yes: normalize
	# no : usually no need to normalize
std = np.std(X_centered, axis=0)
X_centered = X_centered / std
 
# compute unit eigenvectors and eigenvalues of X^TX.
cov_matrix = X_centered.T @ X_centered / (X_centered.shape[0])
eigvals, eigvecs = np.linalg.eigh(cov_matrix)
 
# Sort eigenvalues (and corresponding eigenvectors) in descending order
# note: 189 uses the reversed of the following order (ascending order)
sorted_indices = np.argsort(eigvals)[::-1]
eigvals = eigvals[sorted_indices]
eigvecs = eigvecs[:, sorted_indices]
 
# Choose k. (Optional: use eigenvalues to gauge the optimal k)
k = 3
 
# For the best k-dimensional subspace, pick eigenvectors
top_k_eigvecs = eigvecs[:, :k] # (d, k)
 
# compute the k principle coordinates x.v_i of each training / test point.
X_pca = X_centered @ top_k_eigvecs # (n, k)
 

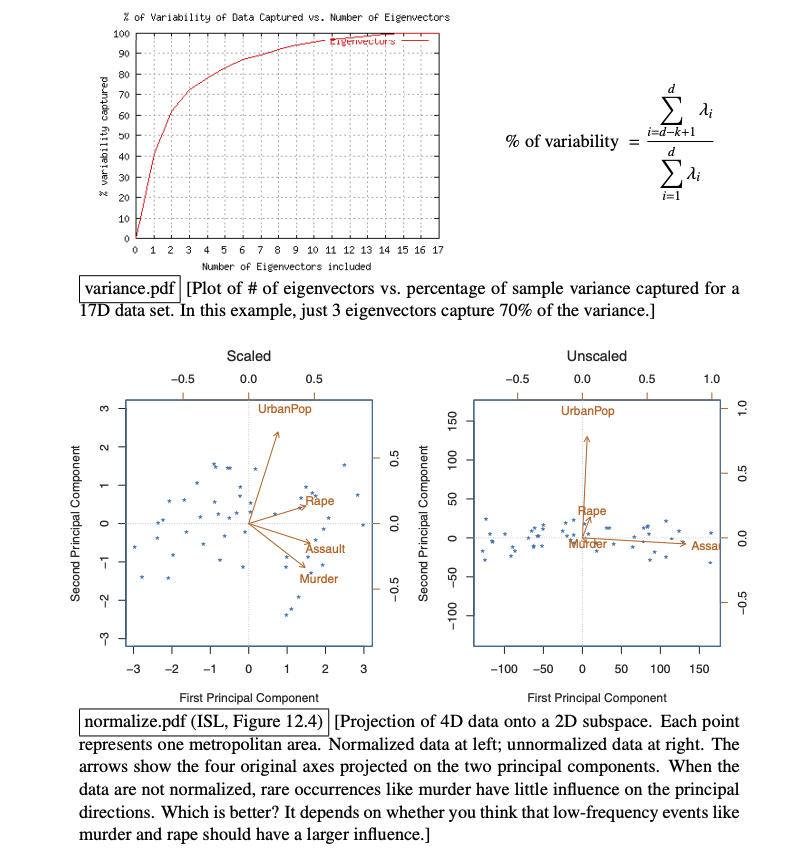
How to choose number of principal components and whether or not to normalize data before doing PCA.

---

Applications

• John Novembre: Genes mirror geography within Europe link
• EigenFaces (Face Recognition)
  • Suppose we have Xcontains n images of faces and d pixels each.
  • Face recognition: Given a query face, compare it with all training faces; find the nearest neighbor in ${\mathbb{R}}^d$.
  • Runtime for each query: $O(nd)$
  • Solution: Run PCA on faces and project onto d' subspaces where $d^{\prime }<d$.
  • The new Runtime: $O(n{d}^{\prime })$
  • If you have 500 stored faces with 40,000 pixels each, and you reduce them to 40 principal components, then each query face requires you to read 20,000 stored principal coordinates instead of 20 million pixels.
  • Eigenfaces encode both face shape and lighting. Some people say that the first 3 eigenfaces are usually all about lighting, and you sometimes get better facial recognition by dropping the first 3 eigenfaces.