Generalization for Neural Networks

1. Get more data
2. Data augmentation (Cat example; rotation, exposure, etc. cutout, mixup, pixmix)
   1. Data augmentation can improve clean accuracy.
      1. 10x increase in model size (weights).
      2. 1000x increase in labeled data.
3. Subset Selection
   1. Eliminate features with un-predictive power.
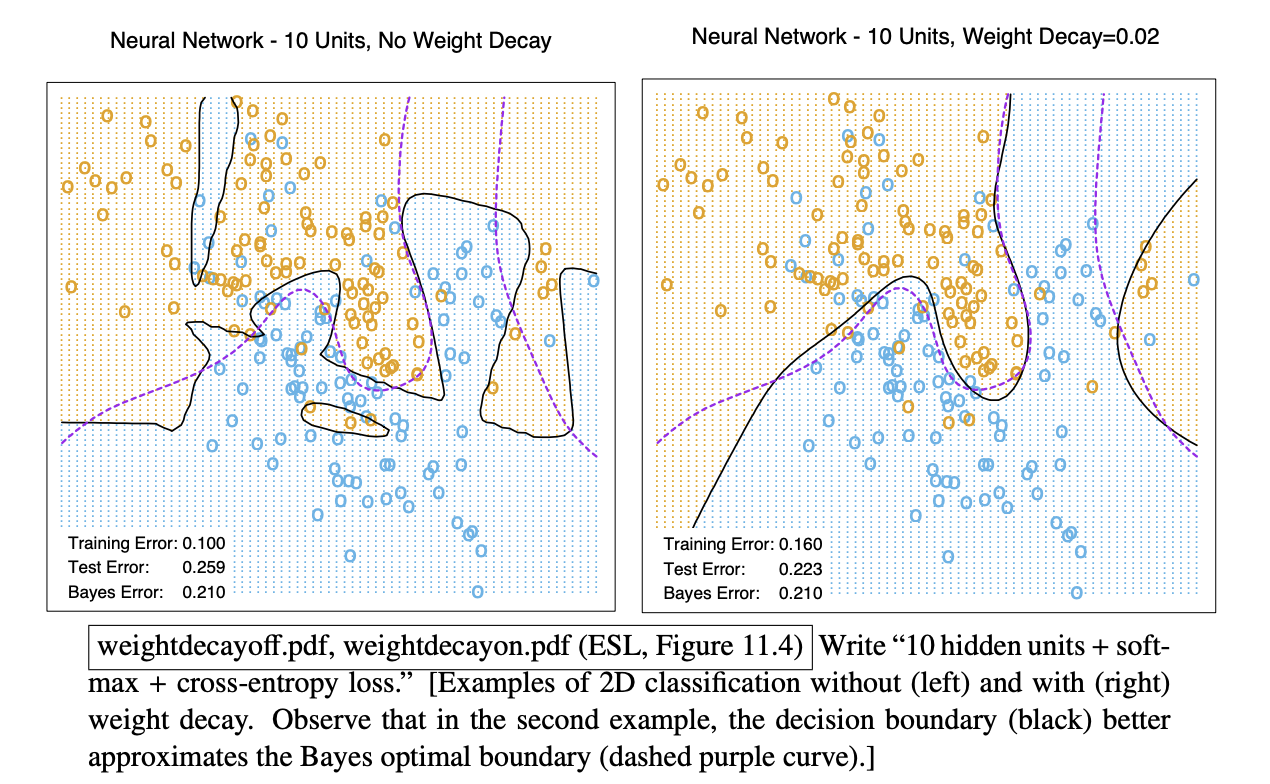
4. $l_2$ regularization | weight decay
   1. add $\lambda \Vert w{\Vert }^2$ to the cost / loss function, where $w$ is the vector of all weights in neural network.
   2. Penalizing the bias term may help for hidden layers.
   3. With the $l_2$ regularization, the gradient will have an extra term $2\lambda w$.
      1. $\nabla w_i=ϵ\frac{dJ}{d{w}_i}$
      2. The weight decays by a factor of $1-2ϵ\lambda$ if not reinforced by training.
      3. The term $\lambda w$ pulls the weights toward zero during every update.
      4. 
      5. AlexNet is a famous example of a network that used both l2 regularization and momentum. Just add the l2 penalty to the cost function J and plug that cost function into the momentum algorithm. AlexNet set $\lambda$= 0.0005 and the momentum decay term to $\beta$ = 0.9. They adjusted $ϵ$ manually throughout training.]
5. Train for a very long time.
6. Ensemble of Neural Networks (2 - 3%)
   1. Random initial weights + SGD + (optionally) bagging.
7. Dropout emulates an ensemble in just one network.
   1. 
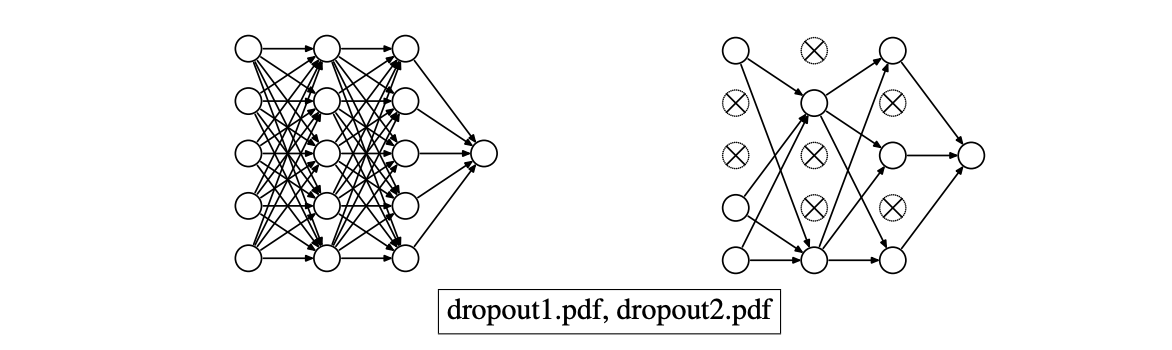
   2. No forward signal, no weight updates for edges in or out of the disabled neuron.
   3. Disable each hidden uint with p = 0.5
   4. Disable each input unit with p = 0.2
   5. Disable a different random subset for each SGD minibatch.
   6. After training, before testing, enable all units. If units in a layer were disabled with probability p, multiply all edge weights out of that layer by p.
   7. “Recall Karl Lashley’s rat experiments, where he tried to make rats forget how to run a maze by introducing lesions in their cerebral cortexes, and it didn’t work. He concluded that the knowledge is distributed throughout their brains, not localized in one place. Dropout is a way to force neural networks to distribute knowledge throughout the weights.”
   8. “Dropout usually gives better generalization than l2 regularization. Geoff Hinton and his co-authors give an example where they trained a network to classify MNIST digits. Their network without dropout had a 1.6% test error; it improved to 1.3% with dropout on the hidden units only; and further improved to 1.1% with dropout on the input units too.”

---

Double Descent

• The problem of falling into the local minima has been solved by making the network bigger.
• Add more layers | more neurons in hidden layer.
• If your layers are wide enough, and there are enough of them, a well-designed neural network can typically output exactly the correct label for every training point, which implies that you’re at a global minimum of the cost function.
• This phenomenon is known as interpolating the labels. i.e. $\hat{y}=y$.
• The agreement today is that if you fall into local minima, the network is not large enough.
• 

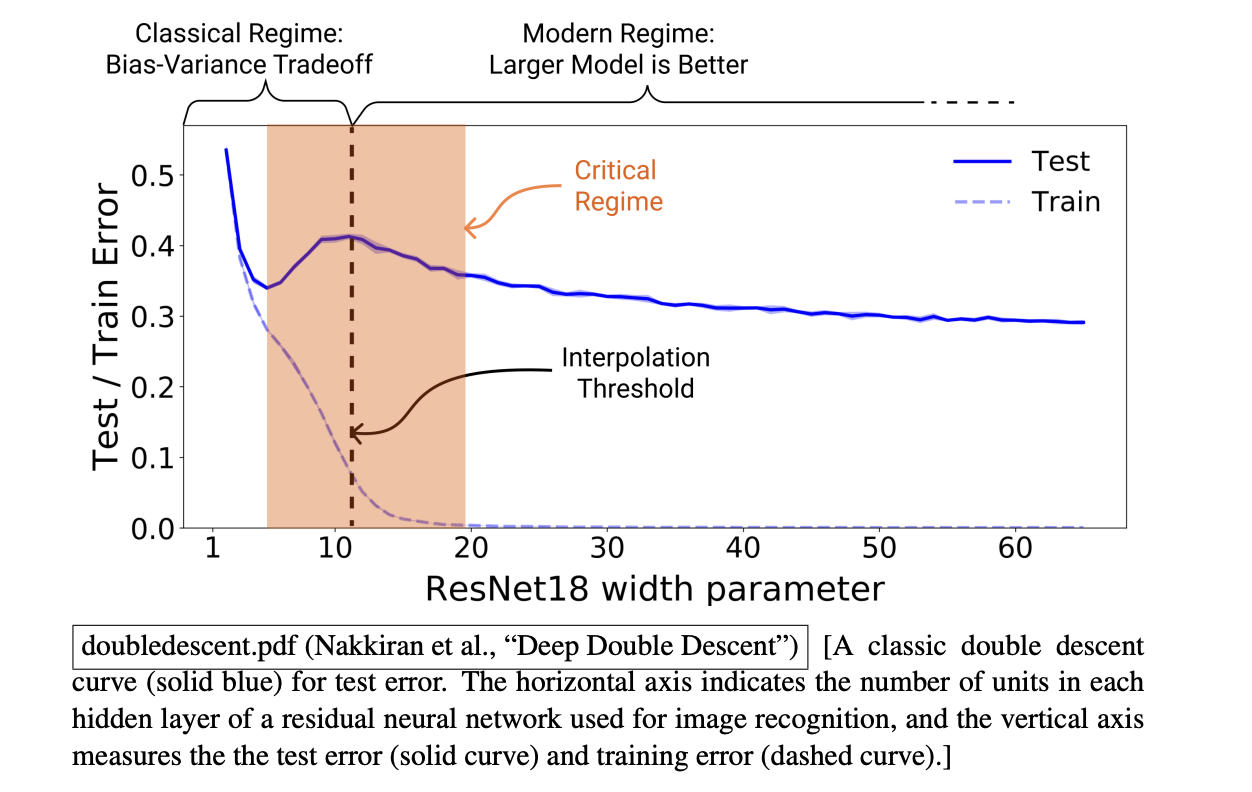
when we pass the point where the network is interpolating the labels and continue to add more weights, we sometimes see a second “descent,” where the test error starts to decrease again and ultimately gets even lower than before!

• The peak in the middle of the curve is larger if we have noise in the labels. Noise will make it harder for the model to fit it exactly.

Nakkiran (Author of Double Descent)

At the interpolation threshold, the model is just barely able to fit the training data; forcing it to fit even slightly-noisy or mis-specified labels will destroy its global structure, and result in high test error.

For over-parameterized models, there are many interpolating models that fit the training set and SGD is able to find the one that “absorbs” the noise while still performing well on the distribution.

There are many possible ways to fit the data exactly when the model is very large. The solution space is large. SGD tends to find solutions that both fit the data and still generalize well, meaning it absorbs the noise without overfitting it in a destructive way.