Vanishing Gradient Problem (ReLUs)

Problem: when unit output s is close to 0 or 1 for most training points, $s^{\prime }=s(1-s)$ is going to be very small making the gradient descent very slow and not efficient. Unit is Stuck | Slow Training. (We don’t want the data to be in the flat spot). Also, the middle part (non-flat) part is kinda like a linear region. We want neural networks to have non-linear activation functions.

Sigmoid and its issues

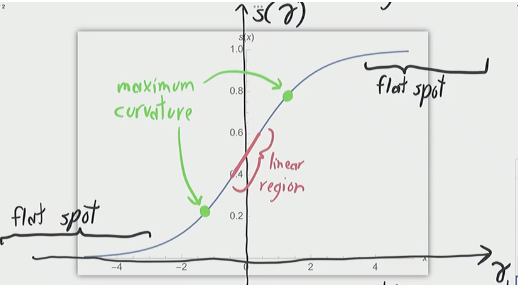
Solution: Replace Sigmoids with Rectified Linear Units (ReLUs)

Rectified Linear Units (ReLUs)

$$\begin{array}{rl}r(x)& =max(0,x)\\ r^{\prime }(x)& =\{\begin{array}{l}0ifx<0\\ 1ifx\ge 0\end{array}\end{array}$$

def relu(x):
	return np.maximum(0, x)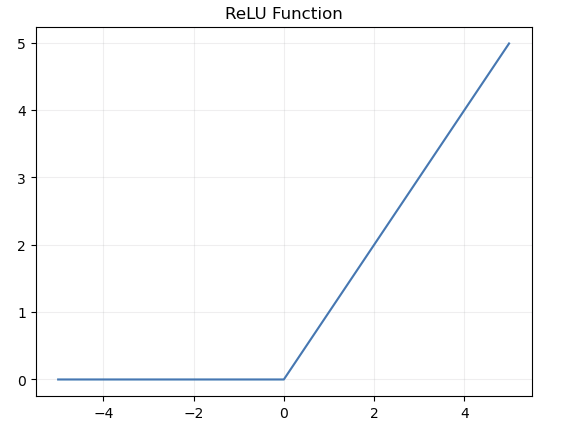

Sub-gradient at x = 0 is not a very big problem.

• In ReLU, Exploding Gradient can be a problem in Deep Neural Network.
• Although it’s mostly linear, in practice, it gives enough non-linearity.
• Most Neural Network today use ReLU Function as Hidden layers.
• ReLUs can get stuck too just like sigmoid functions; but it is rare in practice.

Output Units: chosen to fit the application unlike the hidden layers.

• Regression: Linear regression (Last Layers)
• Classification: Sigmoid (2 class) | Softmax (multi-classes)

---

Output Units

Regression

The activation function is the identity function. Usually trained with squared error loss. So, it is equivalent to doing least squares linear regression on learned features (hidden units). Loss function: Squared Error Loss

Binary Classification (Sigmoid)

Given vector h of unit values in the last hidden layer, output layer computes pre-activation value $a=Wh$, and the applies sigmoid activation function $s(Wh)$ to obtain the prediction $\hat{y}=s(Wh)$.

Loss function: Logistic Loss | Fixes the vanishing gradients at output (because of the shape of logistic loss).

K-class classification (Softmax)

• $y\in R^k$ be a vector of labels for training point x.
• Choose training labels so that ${\sum }_{i=1}^k{y}_i=1$
• One-hot encoding Given hidden layer h output layer computes pre-activation value $a=Wh$ and applies softmax activation to obtain prediction $\hat{y}$ , where

$${\hat{y}}_i(a)=\frac{e^{a_i}}{{\sum }_{j=1}^k{e}^{a_j}}$$

Loss function: cross-entropy loss | Fixes the vanishing gradient problem at the output.

$$L(\hat{y},y)=-\sum _{i=1}^k{y}_i\ln {\hat{y}}_i$$

Different in a way that the $y_i$ are dependent on each other if you compare it to the prediction from sigmoid for example.

---

output + loss	linear + squared error	sigmoid + logistic loss	softmax + cross entropy loss
$\hat{y}$, $L(\hat{y},y)$	$\hat{y}=Wh$ ; $L=\Vert \hat{y}-y{\Vert }^2$	$s(Wh)$ ; $L=-{\sum }_i(y_i\ln {\hat{y}}_i+(1-y_i)\ln (1-{\hat{y}}_i))$	$\hat{y}=softmax(Wh)$ ; $L=-{\sum }_i{y}_i\ln {\hat{y}}_i$
${\nabla }_{w}L$	$2(\hat{y}-y)h^T$	$(\hat{y}-y)h^T$	$(\hat{y}-y)h^T$
${\nabla }_{h}L$	$2W^T(\hat{y}-y)$	$W^T(\hat{y}-y)$	$W^T(\hat{y}-y)$ assuming $\sum y_i=1$

---

Backpropagation

$$V=\left[\begin{array}{ccc}{V}_{11}& V_{12}& V_{13}\\ V_{21}& V_{22}& V_{23}\end{array}\right]$$ $$V_1=\left[\begin{array}{c}{V}_{11}\\ V_{21}\end{array}\right]$$ $$V_1^T=\left[\begin{array}{ccc}{V}_{11}& V_{12}& V_{13}\end{array}\right]$$ $$V_1^{T}x=\left[\begin{array}{ccc}{V}_{11}& V_{12}& V_{13}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]$$