Hierarchical Clustering

In k-means clustering, we must commit to a number k before the algorithm starts. If we pick the wrong k, the algorithm will try to force the data to fit into k disjoint groups — wether it makes natural sense or not.

In Hierarchical Clustering, the advantage is that we don’t need to specify k beforehand. We build a full tree based on a specific technique, and pick a cut height and instantly get those clusters.

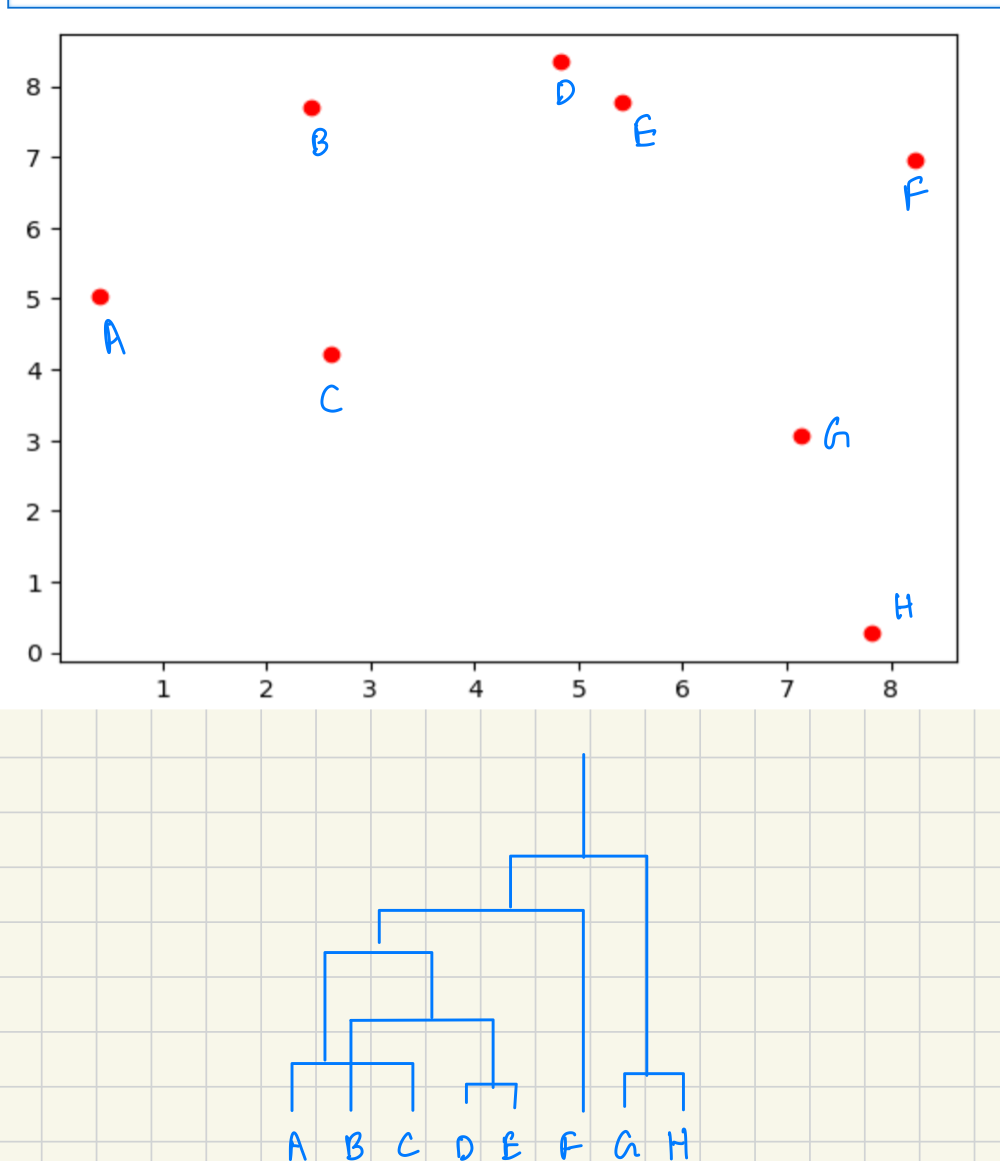
Hierarchical Clustering creates a tree and every subtree is a cluster. (Some clusters might contain smaller clusters. Not all trees will be balanced).

---

Types of Hierarchical Clustering

1. Bottom-up | Agglomerative Clustering
2. Top-down | Divisive Clustering

• When the input is a point set, agglomerative clustering is used much more in practice than divisive clustering.
• When the input is a graph, we use divisive clustering more often.

But, How do we put the points into clusters? We need some sort of measures.

Distance function for Clusters A and B

These distances are called linkage.

1. Complete Linkage: $d(A,B)=max\{dist(a,b);a\in A,b\in B\}$
2. Single Linkage: $d(A,B)=min\{dist(a,b);a\in A,b\in B\}$
3. Average Linkage: $d(A,B)=\frac{1}{|A||B|}{\sum }_{a\in A}{\sum }_{b\in B}dist(a,b)$
4. Centroid Linkage: $d(A,B)=dist({\mu }_A,{\mu }_B)$

Warning

• The first three linkages work for any distance function, even if the input is just an adjacency matrix with distances.
• The centroid linkage only makes sense for $l_2$ Euclidean distance.

---

Greedy Agglomerative Algorithm

1. Repeatedly fuse the two clusters that minimize the linkage d(A, B).
2. Naively takes $O(n^3)$ time.
3. For complete and single linkage, CLINK and SLINK can run in $O(n^2)$ time.

---

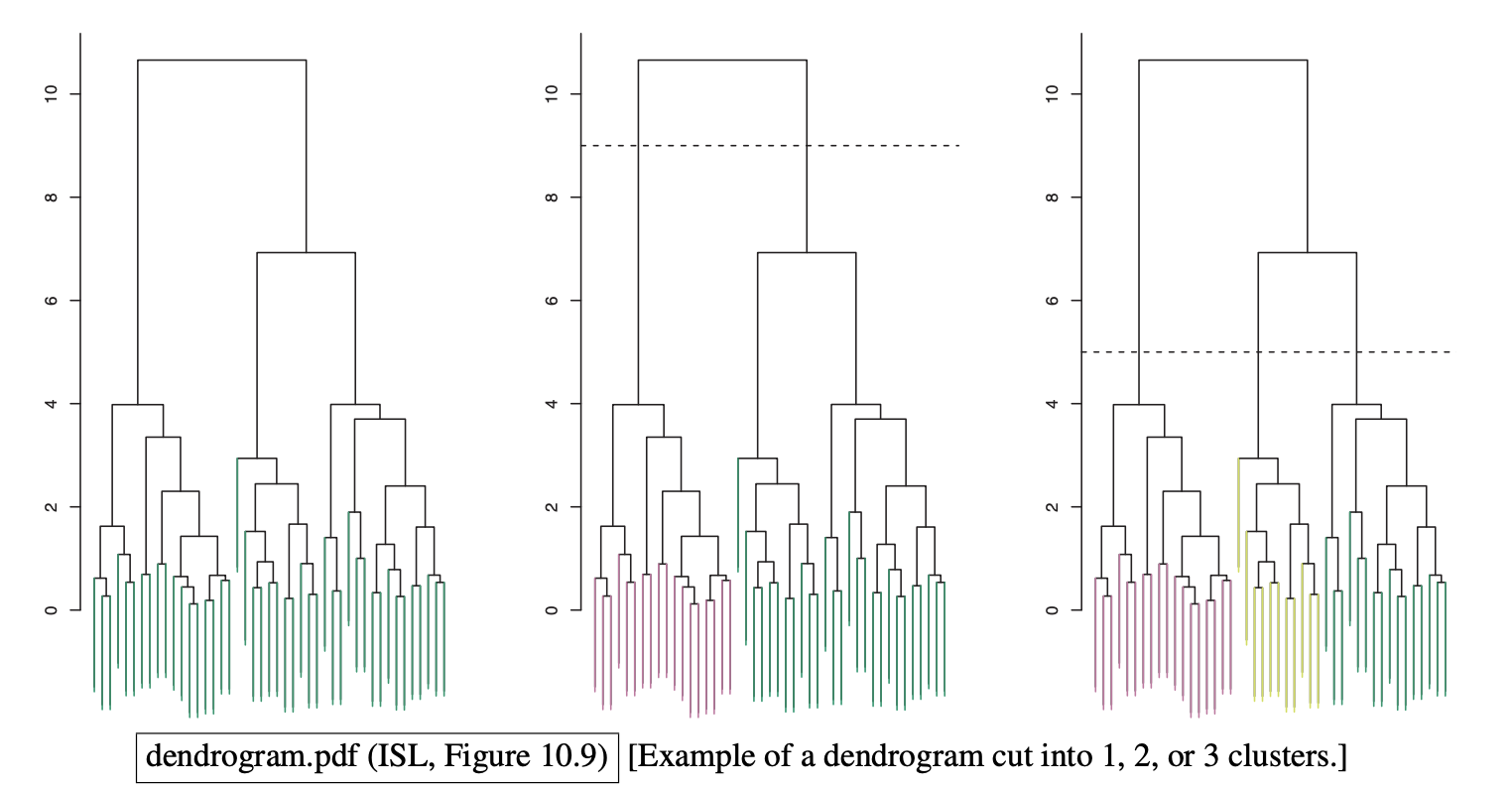
Dendrogram

Cut dendrogram into clusters by horizontal line according to the number of clusters or the intercluster distance.

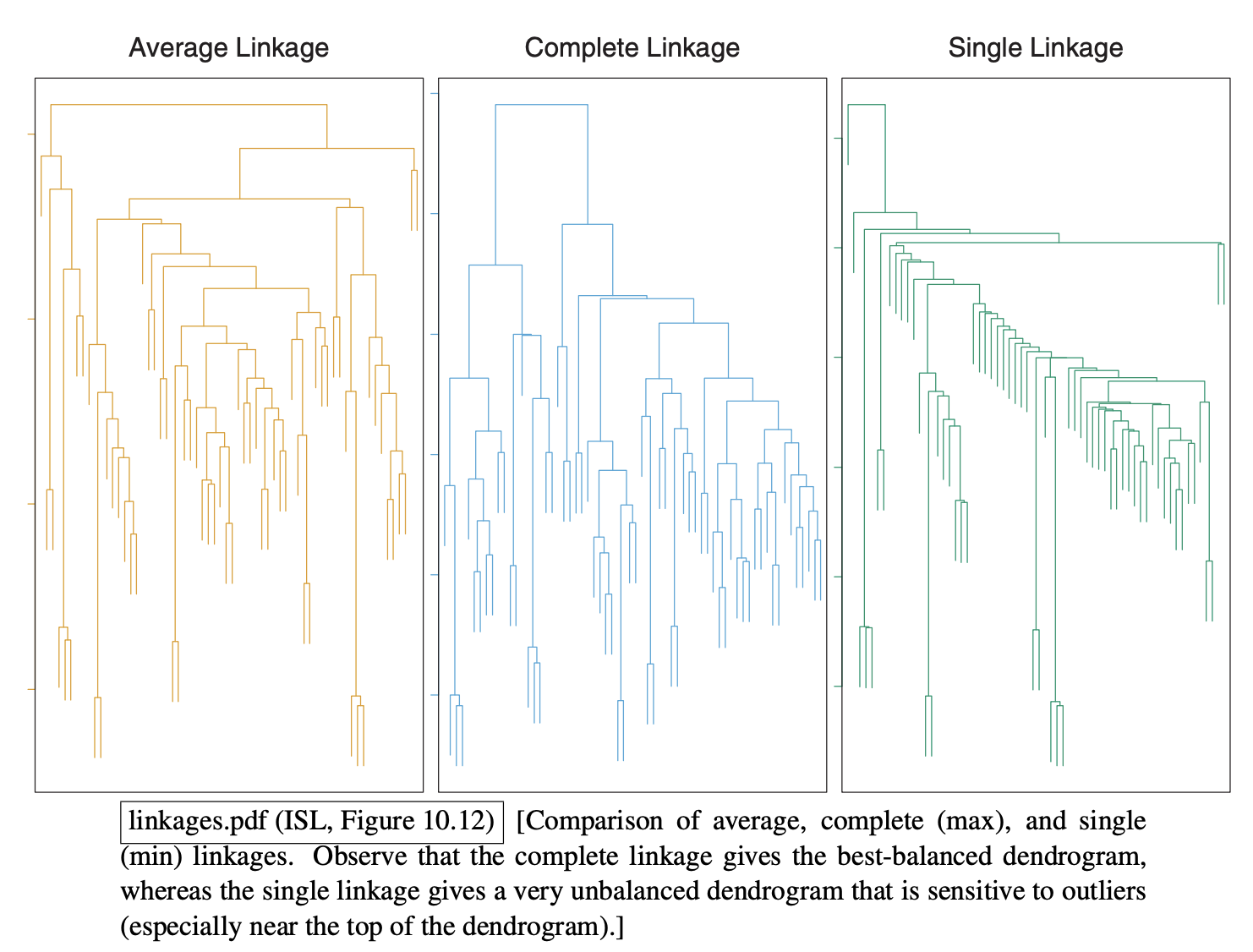
• Notice that the single linkage is prone to outliers and give very unbalanced trees. (e.g. k = 3 cut).
• The complete tends to be the best balanced. When a cluster gets bigger, the farthest point in the cluster is always far away. If balanced clusters is what we want, we should use max distance / complete linkage.
• In most applications, one use average or complete linkage.
• Centroid linkage can cause inversions where a parent cluster is fused at a lower height than its children. Centroid linkage is popular in genomics.

Jonathan Richard Shewchuk

As a final note, all the clustering algorithms we’ve studied so far are unstable, in the sense that deleting a few sample points can sometimes give you very different results. But these unstable heuristics are still the most commonly used clustering algorithms. And it’s not clear to me whether a truly stable clustering algorithm is even possible.

---