K-Means Clustering

Clustering is partitioning data into clusters so that points within a cluster are more similar than across clusters. This is an unsupervised learning method.

Examples:

1. Customer Segmentation
2. Image Compression
3. Songs Recommendation
4. Genetics and bioinformations

Lloyd’s Algorithm - k-Means Clustering

Goal:

• Partition n points into k disjoint clusters.
• Assign each sample point into a cluster label $y_i\in [1,k]$
• Cluster i mean is ${\mu }_i=\frac{1}{n_i}{\sum }_{y\in \{i\}}{x}_i$ given there are $n_i$ points in the cluster $i$.
• Find y that minimizes:

$$\sum _{i=1}^k\sum _{y_j=i}\Vert x_j-u_i{\Vert }^2$$

1. The inner summation is the sum of norm of all points to their cluster mean. (norm of one cluster).
2. The outer summation is the sum of all the cluster norms.

This problem is NP Hard meaning the algorithm will take at least exponential runtime to find the optimal solution.

In this specific problem, the runtime is $O(n{k}^n)$ time, partition all possible combinations.

---

K-means Heuristic Algorithm

Instead of solving for the optimal solution shown in the previous section, we will focus on getting a suboptimal solution:

Alternate between

1. $y_j^{\prime }s$ are fixed; update $u_i^{\prime }s$. | Don’t change label assignments, find the mean
2. $u_i^{\prime }s$ are fixed; update $y_j^{\prime }s$. | Don’t change the means, update the labels (in the sense that we minimize the objective norm. Don’t change the label unless the distance to new mean strictly minimizes).
3. If Step 2 changes no assignments, halt the algorithm.

• So, we have an assignment of points to clusters. (will talk about how to do initial assignment later).
• We compute the cluster means.
• Then we reconsider the assignment.
• A point might change clusters if some other’s cluster’s mean is closer than its own cluster’s mean.
• Then repeat.

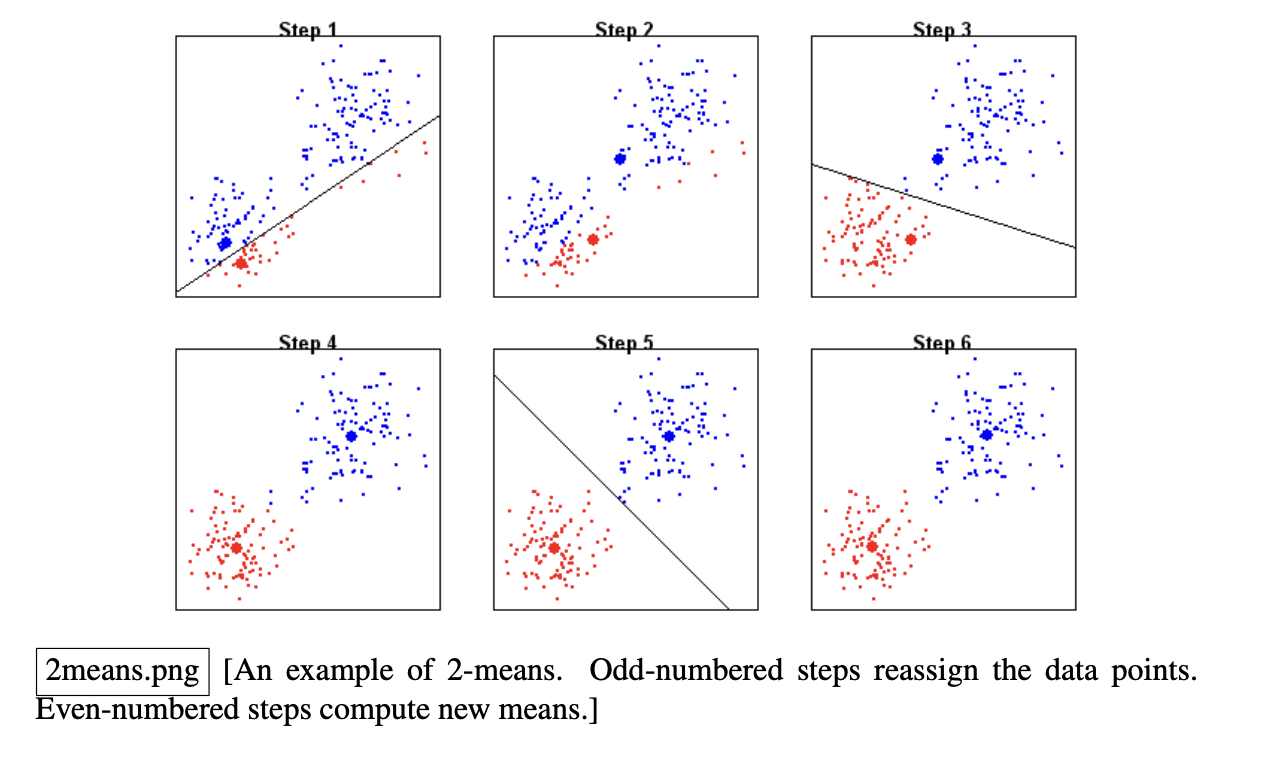
• Step 1: Drop random sample mean, and assign labels
• Step 2: Recalculate the mean
• Step 3: Reassign labels based on the new mean
• Step 4: Recalculate the mean
• Step 5: Reassign labels based on the new mean
• Step 6: RE calculate the mean

Video Visualization: https://www.youtube.com/watch?v=nXY6PxAaOk0&t=40s To Learn More: https://medium.com/@jwbtmf/visualizing-data-using-k-means-clustering-unsupervised-machine-learning-8b59eabfcd3d

Notes on the Heuristic Algorithm

1. Both steps decrease the objective cost function unless they change nothing which is when the algorithm terminates. Thus, algorithm will never return to a previous assignment.
2. Algorithm always terminate as there are only finitely many assignments.
3. However, the algorithm does not guarantee anything about the optimality. We will see $O(k^n)$ different assignments before halt. Therefore, in theory, it is possible to construct points that will take an exponential number of iterations, but not very often in practice. (similar to Simplex Method in LP).
4. In practice, the algorithm runs very fast, and generates a suboptimal solution.

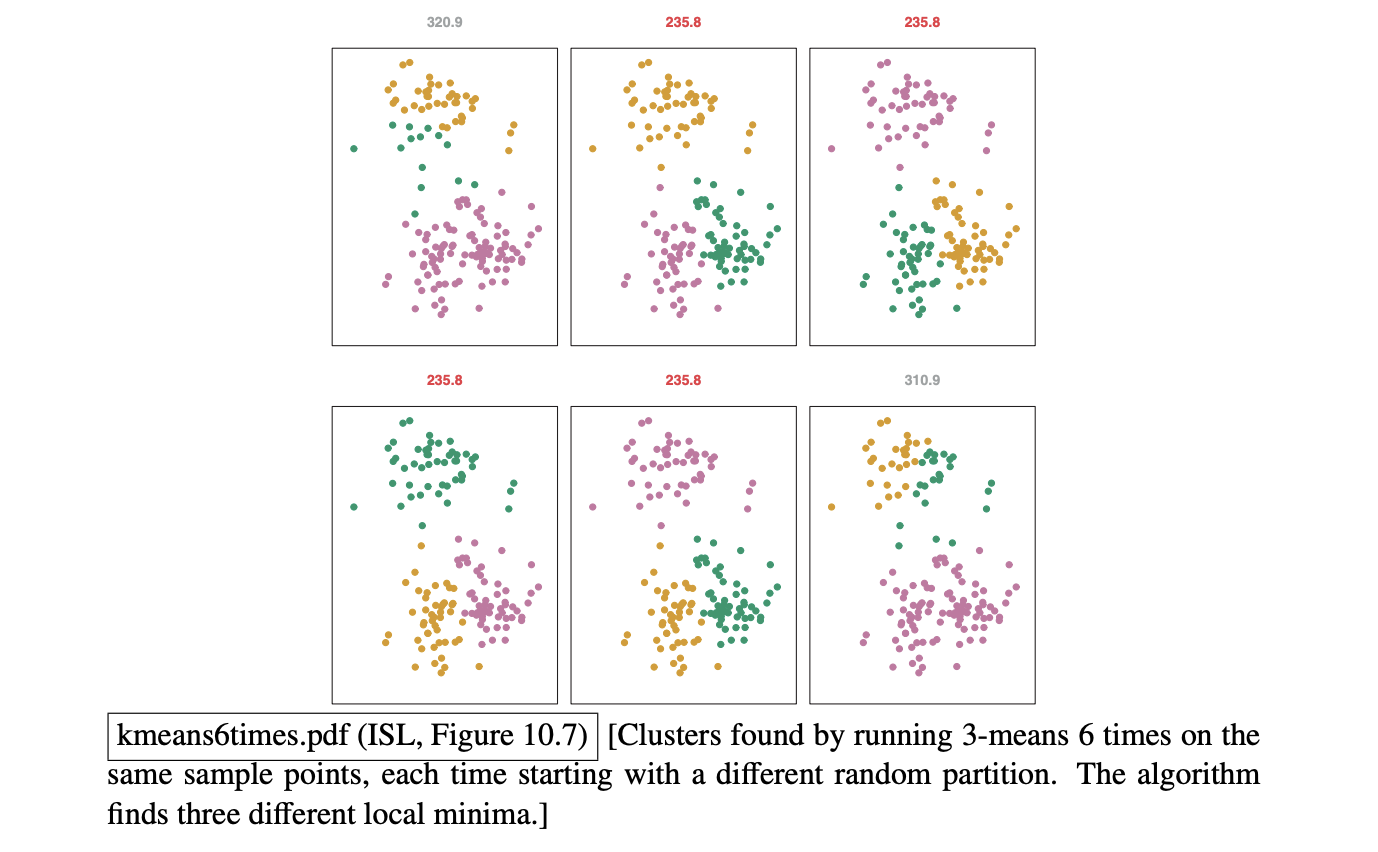
Failed Example

---

How do we initialize the algorithm?

1. Forgy Method: Choose k random sample points to be the initial mean $u_i$. → step 2.
2. Random Partition: Random label assignment to every sample → step 1.
3. K-Means++: Forgy but with biased distribution. Each $u_i$ is chosen with a preference for points far from the previously assigned $u_{i-1}$.

Depends on dataset, but k-means++ works well in practice and theory.

For best results in practice though, we can run k-means multiple time with different initializations and choose the best.

---

Notes on the objective function

---

Data preparing before k-means algorithm?

• Normalization: Same as PCA, sometimes yes, sometimes no.
• Typically, we would want to look at the units and decide whether it makes sense or not to normalize.
• Decide the number of clusters k (domain knowledge).
• One difficulty with k-means is that you have to choose the number k of clusters before you start, and there isn’t any reliable way to guess how many clusters will best fit the data.
• Hierarchical Clustering builds a full tree (dendrogram) of the data, and thus we don’t need to specify the k beforehand.

---

Hierarchical Clustering